دانلود فایل کامل بررسی فنون ديگري براي جمع آوري محصول Partial
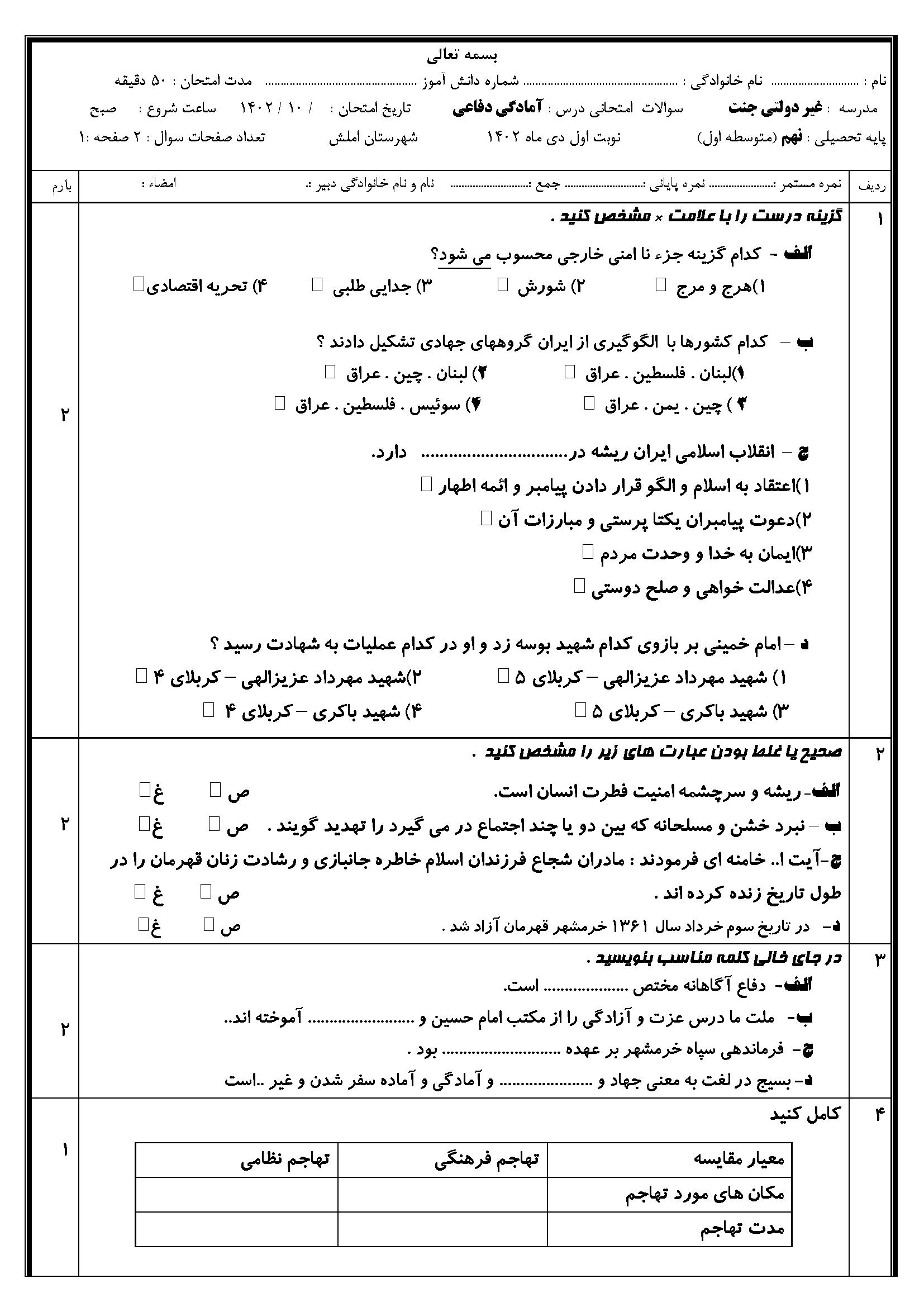
در قالب فایل word و متشکل از 23 صفحه قابل ویرایش ؛
بخشی از محتوا ::
چندين تكنيك ديگر براي اصلاح ساختار درختان CSA معرفي شده است كه از كنتورهاي ۳۰۲ براي رسيدن به طرح منظم تر و Lass arebconsuming استفاده مي كند. چنين ساختارهاي درختي اصلاح شده ممكن است مستلزم تعداد بيشتري از سطوح CSA با تأخير كلي بيشتر باشد. دو نمونه از اين فنون بعداً تشريح مي شود. نمونة اول، درختان تأخير موازنه شده [۲۴] ( همچنين با ۱۹ رجوع شود) را تعيين مي كند در حاليكه نمونة دوم، درختان پلكان واژگون را تعيين مي كند
[۱۵] . شكل ۱۳- ۶ ساختار bit – slices را براي دو تكنيك نشان مي دهد و آنها را با Wallace tree bit8slice متناظر مقايسه مي كند. تمام bit – slices در شكل ۱۳- ۶ براي ۱۸ operands است كه ممكن است بوسيله الگوريتم بزرگ مضاربه اي پايه توليد شود. در اين مورد، ۱۸ مثلث واژگون در شكل ۱۳-۶ ۳و ۲ هستند و اعداد روي اين كنتورها، تأخير تجربه شده توسط operands داده را نشان مي دهند. بنابر اين ع پس از اينكه نتايج ۲~ ۶۴ توسط Wallae و درختان پلكان واژگون توليد شدند، درخت متوازن مستلزم ~ AFA است.
توجه كنيد كه تمام ۳ ساختار درختي ، شامل ۱۵ Carries حاصل بيرون رونده و ۱۵ حاصل وارده شونده هستند و هر حامل بيرون رونده در مسير حامل وارد شوندة خود قرار دارد، براي اينكه با bit – slices مجاور ، متصل شود. حاملان وارد شونده با كنتورهاي مختلف (۳ و ۲۹ ronted درگير مي شوند، براي اينكه تمام داده ها به يك كنتور قبل يا در زمان لازم معتبر هستند . تنها براي درختان متوازن تمام ۱۵ حامل وارد شوندهه هنگامي كه لازم هستند به طور كامل توليد مي شوند چون تمام مسيرها متوازن هستند در ۲ درخت ديگر، كنتورهايي وجود دارد كه تمام حاملان وارد شوند به طور همزمان توليد نشوند. براي مثال، منتور پاييني در درخت پلكان واژگون ، حاملان وارد شونده اي دارد كه تأخيرهاي مرتبط،۴۴ و۵۴ هستند.
۳ ساختار درختي همچنين در تعداد مسير كشي لازم بين bit – slices مجاور متفاوت هستند، اين در عوض بر مساخت طرح اثر مي گذارد. درخت Wallae مستلزم ۶ مسير سيم كشي است، پلكان واژگون و درخت متوازن به ترتيب مستلزم ۳ و ۲ مسير هستند. به رابطة trabeoff لاينفك بين اندازه و سرعت توجه فرمائيد. درخت Wallae، پائين ترين تأخير كلي را تضمين مي كند اما بيشترين تعداد مسيرهاي سيم كشي است.
درخت متوازن، از سوي ديگر، مستلزم كمترين تعداد مسير سيم كشي است اما بيشترين تأخير كلي را دارد. درختان متوازن و پلكان واژگون ساختار منظمي دارند و مي توانند به روش قانونمندي طراحي شوند اين به سختي از شكل ۱۳- ۶ ديده مي شود، اما از شكل ۱۳- ۶ كه ساختار كامل دو درخت را مانند آن درخت Wallae متناظر نشان مي دهد مي توان نتيجه گيري كرد. آجرهاي ساختمان درختان متوازن و پلكان واژگون، با خطوط منظم و برخي انحرافات آنها مي توانند از ۱۲۴۱ و [۱۵] مشخص شوند. در هنگام تعيين طرح نهايي يك درخت SCA، بايد دقت شود تا اطمينان حاصل شود كه سيم ها، داده ها را به Carry – Save adder با طولي تقريباً مشابه وصل مي كنند، در غير اينصورت مسيرهاي متوازن تأخير ديگر متوازن نخواهند بود.
براي مثال ، يك درخت CSA را براي ۲۷ محصول operands بدست آمده از bit – ۵۳ افزاينده با استفاده از الگوريتم اصلاح شدة پاية Booth 4، يك درخت CSA از كمپرسورهاي ۲ و ۴ نشان داده شده در شكل ۱۵- ۶ ساخته مي شود و طرح متناظر در شكل ۱۵ – ۶ (ب) ۱۲۵۱ نشان داده شده است. توجه كنيد كه كمپرسور پائيني (۱۳# در وسط قرار دارد، براي اينكه كمپرسورهاي ۱۱# و ۱۲# در فاصله نسبتاً مشابهي از آن هستند. كمپرسور ۱۱# در عوض سيم هايي با طول مشابه از ۸# و ۹# و … دارد.)
• ۵ – ۶ واحد افزودن مضرب تركيبي (FMA)
يك واحد FMA، ضرب A * B زير را فوراً بوسيله يك محصول اضافي و operand سوم (C) انجام مي دهد براي اينكه محاسبه A * b + C يك عمل واحد و منفرد انجام مي گيرد. واضح است كه چنين واحدي قادر به انجام ضرب تنها با قرار دادن C=0 و جمع (يا تفريق) تنها با قرار دادن براي مثال B=1 مي باشد.
يك واحد FMA مي تواند زمان كلي استخراج ضرب زنجيره اي ۰ را كاهش دهد وسپس عمليات تفريق را اضافه نمايد. يك مثال براي اين مورد زماني كه اين ضرب و جمع زنجيره اي مفيدند، در ارزيابي چند اسمي an * n + a , -1 * n-1 + … + aa از طريق{(GX + an -1) X + an -2} X + … است. از سوي ديگر ، ضرب مستقل و عمليات جمع نمي توانند به موازات هم انجام گيرند.
مزيت ديگر يك واحد FMA در مقايسه با افزاينده و جمع كنندة مجزا، زمان اجراي عمليات نقطة شناور است، چون گرد كردن تنها يكبار براي نتيجه A * B + C انجام مي گيريد نه دوبار (ضرب وسپس براي جمع). چون گرد كردن ممكن است خطا هاي محاسبه را نشان دهد، كاهش تعداد گرد كردن ها ممكن است اثر مثبتي بر خطاي كلي داشته باشد. در طرح گزارش شده در ۱۱۴۱، اين صحت اضافي زماني مفيد بود كه به طور صحيحي خارج قسمت را در تقسيم بر الگوريتم متناوب گرد كند. (رجوع شود به بخش ۲ – ۸).
شكل ۱۶- ۶ اجراي يك واحد FMA را براي محاسبات نقطة شناور نشان مي دهد. در اينجا C , B , A قابل توجه هستند در حاليكهE c ,Eg , Eaبه تركيب نمونه هاي operands هستند درخت CSA تمام محصولات نسبي را توليد مي كند و جمع آوري Carry – Save را براي توليد ۲ نتيجه اي كه سپس با operand مرتب شدة C به طور صحيح جمع مي شود. جمع كنندة ۳ operands را مي پذيرد و بنابر اين، ابتدا بايد آنها را به ۲ (با استفاده از كنتورهاي ۲ و ۳) كاهش دهد و
سپس افزايش حمل – تكثير را انجام مي دهد. مراحل طرح و نرمال سازي و گرد كردن سپس انجام مي گيرند. طرح نشان داده شده در شكل ۱۶- ۶ ، ۲ تكنيك را براي كاهش زمان اجراي كلي بكار مي برد. ابتدا، مدار مهم پيش بيني كنندة صفر، از تكثير استفاده مي كند و علائم توليد شده توسط adder را براي پيش بيني نوع تغييري كه در مرحله پس از نرمال سازي مورد نياز است، توليد كند. اين مدار به موازات خود جمع عمل مي كند براي اينكه تأخير مرحلة نرمال سازي كوتاه تر است. ثانياًو مهمتر اينكه ، مرتب كردن C برجسته در Ea + Eg – Ec به موازات ضرب A و B انجام مي گيرد. به طور معمول، يك جمع نقطة شناور، ما اهميت
operand كوچك تر را مرتب مي كنيم. اين دلالت دارد بر اينكه اگر محصول AXBكوچكتر از C باشد. بايد محصول را پس از توليد، تغيير دهيم و تأخير اضافي را نشان دهيم. ترجيح مي دهيم هميشه C را مرتب كنيم حتي اگر بزرگتر از AXB باشد، تا تغيير به موازات ضرب باشد. براي رسيدن به اين ، بايد اجازه دهيم كه C به راست يا چپ تغيير كند (مسيري كه به ترتيب با مثبت يا منفي بودن نتيجة Ea + EB – Ec ديكته مي شود). اگر اجازه بدهيم C به چپ تغيير كند بايد عدد كلي Bits در adder افزايش يابد. براي مثال ، اگر تمام operands، اعداد نقطة شناور در قالب طولاني IEEE هستند، ترتيب ممكن C در رابطه با محصول AXB به صورت زير نشان داده مي شود.
اين ترتيب براي ۵۳ – ۲ EA + EB – EC 2 53 است. اگر ۵۴ ۲ EA + Eg – EC باشد، بيت هاي C بيشتر به راست تغيير كرده اند، جايگزين بيت چسبنده مي شود و اگر ۵۴-۵ EA + ED – EC باشد تمام بيت هاي A * B جايگزين يك بيت چسبنده مي گردند. بنابر اين penaity جريمة كليع ۵۰ درصد افزايش در پهناي adder مي باشد كه در عوض، زمان اجراي adder را افزايش خواهد داد. به هر حال توجه كنيد كه ۵۳ بيت بالاي adderتنها لازم است قادر به افزايش محتويات اصلي ۵۳ بيت باشد (اگر يك Carry از۱۰۶ بيت پائيني تكثير يابد).
مسير از محصول مدار گردشي در شكل ۱۶ – ۶ به مضرب در سمت راست زماني بكار مي رود كه محاسبه اي نظير (xy + z) + AXB انجام مي شود. مسير از محصول مدار نرمال سازي به مضرب سمت چپ زماني بكار مي رود كه محاسباه اي نظير (X * Y + Z) + C انجام مي شود. در اين مورد مرحلة گرد كردن براي (A * B + C) در زماني مشابه با ضرب در D با افزودن محصول نسبي ۱nn * D به درخت CSA انجام مي گيرد.
• ۶ – ۶ تنظيم مضرب ها در عمل اساسي (توليد محصولات نسبي و جمع) ممكن است ظاهر شوند. در اين روش، از افراطب overhead كه بخاطر كنترل هاي جداگانة اين دو عمل است جلوگيري مي كنيم و بنابر اين سرعت ضرب را بالا مي بريم. اين مضرب ها كه شامل سلولهاي يكساني است كه قارد به تشكيل يك محصول نسبي جديد و افزودن آن به محصول نسبي جمع شده از قبل مي باشد، مضرب هاي كناري ناميده مي شوند. واضح است كه هر سودي در سرعت، به هزينه سخت افزار
اضافي بدست مي آيد. ويژگي مهم ديگر تنظيم مضرب ها اين است كه آنها مي توانند براي حمايت سرعت بالاي لوله كشي بكار روند. براي نشان دادن عمل تنظيم يك مضرب، متوازي الاضلاع ۵ * ۵ نشان داده شده در شكل ۱۷- ۶ را آزمايش مي كنيم كه شامل ۲۵ بيت محصول نسبي به شكل a4 . xjاست كه به طور صحيحي مرتب شده است. يك استنباط مستقيم از تنظيم مضرب، دو محصول نسبي نخست را پس از تنظيم صحيح جمع مي كند. نتايج رديف اول سپس با ad .xz به صورت aD .xz … و ۲۲ در رديف دوم جمع مي شود و …. سلول اصلي براي هر تنظيم مضرب، يك FA مورد قبول يكي از محصولات نسبي جديد (ai . xi) ، يك بيت از محصول نسبي از قبل جمع شده و يك carry – in – bit است. يك نمودار block از يك تنظيم ۵*۵ براي اعداد بدون علامت، در شكل ۱۸ – ۶ ترسيم شده است. در ۴ رديف اول ، هيچ تكثير افقي carry وجود ندارد. به عبارت ديگر، يك نوع افزايش carry – save در اين رديف ها انجام مي گيرد و محصول سبي جمع شده شامل جمع متوسط و بيت هاي carry است.
تنها در رديف آخر ، تكثير افقي carry مجاز است. رديف آخر سلولها در شكل يك ripple carry – adder است كه مي تواند با يك two – operand adder سريع جايگزين شود (اگر زمان اجراي كلي مطلوب باشد) تنظيم مضرب در شكل ۱۶ – ۶ بايد براي ضرب اعداد علامت دار در دو تكميل عدد نويسي اصلاح شود، چون بيت هاي محصولي نظير a4 .xo و ao . x4 ، وزن منفي دارند و بايد كسر شوند نهجمع . يك روش براي كنترل صحيح ۸ بيت محصول نسبي وزن شدة منفي در يك ضرب ۵*۵ بيتي، در شكل ۱۹- ۶ ترسيم شده است. بيت ها با وزن منفي. با يك دايرة كوچك به جاي يك فلش، نشان داده مي شوند. اين بيت ها بايد بجاي جمع ، كسر شوند. سلولهاي با۳ محصول مثبت معمولاً FAS هستند و در شكل با I نشان داده مي شوند. سلولهاي با يك دادة منفي واحد و دو دادة مثبت ، با II نشان داده مي شوند. مجموع ۳ داده از يك سلول نوع II مي تواند از ۱- تا ۲ متغير باشد. اين مستلزم اين است كه محصول ديجيتالي C ، وزني معادل با ۲+ داشته باشد و محصول عمودي S وزن ۱- داشته باشد. عمل جبري يك سلول نوع II به وسيلة معادله با تمام داده هاي منفي نشان داده تشريح مي شود و به طور منفي وزن C و محصولات S را مي گيرد. اين سلول اعداد۱- را در داده هايش مي شمرد و اين عد را از طريق محصولات C و S نشان مي دهد. عمل منطقي آن مانند سلول نوع I است و بنابر اين، اجراهاي gate ورودي آنها يكسان است. اين ، تشريح كنندة دليل علامت گذاري آنها به صورت I , I است . همچنين اجراهاي ورودي سلولهاي نوع II و II يكسان هستند. شيوة ديگر براي طرح يك ضرب منظم براي ۲ مؤلفة operands، استفاده از الگوريتم Booth است. يك مضرب طبق اين الگوريتم شامل n رديف از سلولهاي اصلي است كه n ، تعداد بيت هاي مضرب است. هر رديف قارد به جمع يا كسر مضربهاي مرتب شدة صحيح به محصول نسبي جمع شدة قبلي است. سلولها در رديف C ، جمع يا كسر يا تنها تبديل را بسته به تعداد xi و بيت مرجع مناسب انجام مي دهند. اين مضرب در شكل ۲۰ – ۶ براي operands 4 بيت داده شده است. سلول اصلي در اين مضربع يك مدار كنترل شدة جمع / كسر / تبديل است كه در شكل ۲۰ – ۶ الف) ترسيم شده است [۱۲] . علامت هاي D , H علامت هاي كنترل نشان دهندة نوع عمل براي اجرا توسط رديف متناظر سلولهاي CASS است. اگر H ، صفر باشد هيچ جبري انجام نمي گيرد و بنابر اين بيت محصول نسبي جديد كه توسط Pwt نشان داده شده است برابر با بيت قبلي است.
اگر H=1 باشد يك عمل جبري انجام گرفته است (توليد يك pwt جديد). نوع عمل جبري بوسيلة علامت D نشان داده مي شود. اگر D=0 باشد، آنوقت بيت مضروب كه توسط a نشان داده مي شود، به pin با Q اضافه مي شود كه به عنوان يك بيت حمل وارد شونده از سلول مجاور به سمت راست است. سپس سلول، pont و C و t را به عنوان حمل خارج شونده به سلول بعدي در سمت چپ توليد مي كند. اگر D=1 باشد ، آنوقت بيت مضرب (a) از pin با Q كم مي شود كه به عنوان يك borrow وام خارج شونده است. بنابر اين معادلات قانوني براي c , t , t , p چنين است [۱۲] : pat = pin @ (a.H) @ (Q,.H) و Cat = (oin @ D) . (attim) + A . Gin .
در قالب فایل word و متشکل از 23 صفحه قابل ویرایش ؛
بخشی از محتوا ::
چندين تكنيك ديگر براي اصلاح ساختار درختان CSA معرفي شده است كه از كنتورهاي ۳۰۲ براي رسيدن به طرح منظم تر و Lass arebconsuming استفاده مي كند. چنين ساختارهاي درختي اصلاح شده ممكن است مستلزم تعداد بيشتري از سطوح CSA با تأخير كلي بيشتر باشد. دو نمونه از اين فنون بعداً تشريح مي شود. نمونة اول، درختان تأخير موازنه شده [۲۴] ( همچنين با ۱۹ رجوع شود) را تعيين مي كند در حاليكه نمونة دوم، درختان پلكان واژگون را تعيين مي كند
[۱۵] . شكل ۱۳- ۶ ساختار bit – slices را براي دو تكنيك نشان مي دهد و آنها را با Wallace tree bit8slice متناظر مقايسه مي كند. تمام bit – slices در شكل ۱۳- ۶ براي ۱۸ operands است كه ممكن است بوسيله الگوريتم بزرگ مضاربه اي پايه توليد شود. در اين مورد، ۱۸ مثلث واژگون در شكل ۱۳-۶ ۳و ۲ هستند و اعداد روي اين كنتورها، تأخير تجربه شده توسط operands داده را نشان مي دهند. بنابر اين ع پس از اينكه نتايج ۲~ ۶۴ توسط Wallae و درختان پلكان واژگون توليد شدند، درخت متوازن مستلزم ~ AFA است.
توجه كنيد كه تمام ۳ ساختار درختي ، شامل ۱۵ Carries حاصل بيرون رونده و ۱۵ حاصل وارده شونده هستند و هر حامل بيرون رونده در مسير حامل وارد شوندة خود قرار دارد، براي اينكه با bit – slices مجاور ، متصل شود. حاملان وارد شونده با كنتورهاي مختلف (۳ و ۲۹ ronted درگير مي شوند، براي اينكه تمام داده ها به يك كنتور قبل يا در زمان لازم معتبر هستند . تنها براي درختان متوازن تمام ۱۵ حامل وارد شوندهه هنگامي كه لازم هستند به طور كامل توليد مي شوند چون تمام مسيرها متوازن هستند در ۲ درخت ديگر، كنتورهايي وجود دارد كه تمام حاملان وارد شوند به طور همزمان توليد نشوند. براي مثال، منتور پاييني در درخت پلكان واژگون ، حاملان وارد شونده اي دارد كه تأخيرهاي مرتبط،۴۴ و۵۴ هستند.
۳ ساختار درختي همچنين در تعداد مسير كشي لازم بين bit – slices مجاور متفاوت هستند، اين در عوض بر مساخت طرح اثر مي گذارد. درخت Wallae مستلزم ۶ مسير سيم كشي است، پلكان واژگون و درخت متوازن به ترتيب مستلزم ۳ و ۲ مسير هستند. به رابطة trabeoff لاينفك بين اندازه و سرعت توجه فرمائيد. درخت Wallae، پائين ترين تأخير كلي را تضمين مي كند اما بيشترين تعداد مسيرهاي سيم كشي است.
درخت متوازن، از سوي ديگر، مستلزم كمترين تعداد مسير سيم كشي است اما بيشترين تأخير كلي را دارد. درختان متوازن و پلكان واژگون ساختار منظمي دارند و مي توانند به روش قانونمندي طراحي شوند اين به سختي از شكل ۱۳- ۶ ديده مي شود، اما از شكل ۱۳- ۶ كه ساختار كامل دو درخت را مانند آن درخت Wallae متناظر نشان مي دهد مي توان نتيجه گيري كرد. آجرهاي ساختمان درختان متوازن و پلكان واژگون، با خطوط منظم و برخي انحرافات آنها مي توانند از ۱۲۴۱ و [۱۵] مشخص شوند. در هنگام تعيين طرح نهايي يك درخت SCA، بايد دقت شود تا اطمينان حاصل شود كه سيم ها، داده ها را به Carry – Save adder با طولي تقريباً مشابه وصل مي كنند، در غير اينصورت مسيرهاي متوازن تأخير ديگر متوازن نخواهند بود.
براي مثال ، يك درخت CSA را براي ۲۷ محصول operands بدست آمده از bit – ۵۳ افزاينده با استفاده از الگوريتم اصلاح شدة پاية Booth 4، يك درخت CSA از كمپرسورهاي ۲ و ۴ نشان داده شده در شكل ۱۵- ۶ ساخته مي شود و طرح متناظر در شكل ۱۵ – ۶ (ب) ۱۲۵۱ نشان داده شده است. توجه كنيد كه كمپرسور پائيني (۱۳# در وسط قرار دارد، براي اينكه كمپرسورهاي ۱۱# و ۱۲# در فاصله نسبتاً مشابهي از آن هستند. كمپرسور ۱۱# در عوض سيم هايي با طول مشابه از ۸# و ۹# و … دارد.)
• ۵ – ۶ واحد افزودن مضرب تركيبي (FMA)
يك واحد FMA، ضرب A * B زير را فوراً بوسيله يك محصول اضافي و operand سوم (C) انجام مي دهد براي اينكه محاسبه A * b + C يك عمل واحد و منفرد انجام مي گيرد. واضح است كه چنين واحدي قادر به انجام ضرب تنها با قرار دادن C=0 و جمع (يا تفريق) تنها با قرار دادن براي مثال B=1 مي باشد.
يك واحد FMA مي تواند زمان كلي استخراج ضرب زنجيره اي ۰ را كاهش دهد وسپس عمليات تفريق را اضافه نمايد. يك مثال براي اين مورد زماني كه اين ضرب و جمع زنجيره اي مفيدند، در ارزيابي چند اسمي an * n + a , -1 * n-1 + … + aa از طريق{(GX + an -1) X + an -2} X + … است. از سوي ديگر ، ضرب مستقل و عمليات جمع نمي توانند به موازات هم انجام گيرند.
مزيت ديگر يك واحد FMA در مقايسه با افزاينده و جمع كنندة مجزا، زمان اجراي عمليات نقطة شناور است، چون گرد كردن تنها يكبار براي نتيجه A * B + C انجام مي گيريد نه دوبار (ضرب وسپس براي جمع). چون گرد كردن ممكن است خطا هاي محاسبه را نشان دهد، كاهش تعداد گرد كردن ها ممكن است اثر مثبتي بر خطاي كلي داشته باشد. در طرح گزارش شده در ۱۱۴۱، اين صحت اضافي زماني مفيد بود كه به طور صحيحي خارج قسمت را در تقسيم بر الگوريتم متناوب گرد كند. (رجوع شود به بخش ۲ – ۸).
شكل ۱۶- ۶ اجراي يك واحد FMA را براي محاسبات نقطة شناور نشان مي دهد. در اينجا C , B , A قابل توجه هستند در حاليكهE c ,Eg , Eaبه تركيب نمونه هاي operands هستند درخت CSA تمام محصولات نسبي را توليد مي كند و جمع آوري Carry – Save را براي توليد ۲ نتيجه اي كه سپس با operand مرتب شدة C به طور صحيح جمع مي شود. جمع كنندة ۳ operands را مي پذيرد و بنابر اين، ابتدا بايد آنها را به ۲ (با استفاده از كنتورهاي ۲ و ۳) كاهش دهد و
سپس افزايش حمل – تكثير را انجام مي دهد. مراحل طرح و نرمال سازي و گرد كردن سپس انجام مي گيرند. طرح نشان داده شده در شكل ۱۶- ۶ ، ۲ تكنيك را براي كاهش زمان اجراي كلي بكار مي برد. ابتدا، مدار مهم پيش بيني كنندة صفر، از تكثير استفاده مي كند و علائم توليد شده توسط adder را براي پيش بيني نوع تغييري كه در مرحله پس از نرمال سازي مورد نياز است، توليد كند. اين مدار به موازات خود جمع عمل مي كند براي اينكه تأخير مرحلة نرمال سازي كوتاه تر است. ثانياًو مهمتر اينكه ، مرتب كردن C برجسته در Ea + Eg – Ec به موازات ضرب A و B انجام مي گيرد. به طور معمول، يك جمع نقطة شناور، ما اهميت
operand كوچك تر را مرتب مي كنيم. اين دلالت دارد بر اينكه اگر محصول AXBكوچكتر از C باشد. بايد محصول را پس از توليد، تغيير دهيم و تأخير اضافي را نشان دهيم. ترجيح مي دهيم هميشه C را مرتب كنيم حتي اگر بزرگتر از AXB باشد، تا تغيير به موازات ضرب باشد. براي رسيدن به اين ، بايد اجازه دهيم كه C به راست يا چپ تغيير كند (مسيري كه به ترتيب با مثبت يا منفي بودن نتيجة Ea + EB – Ec ديكته مي شود). اگر اجازه بدهيم C به چپ تغيير كند بايد عدد كلي Bits در adder افزايش يابد. براي مثال ، اگر تمام operands، اعداد نقطة شناور در قالب طولاني IEEE هستند، ترتيب ممكن C در رابطه با محصول AXB به صورت زير نشان داده مي شود.
اين ترتيب براي ۵۳ – ۲ EA + EB – EC 2 53 است. اگر ۵۴ ۲ EA + Eg – EC باشد، بيت هاي C بيشتر به راست تغيير كرده اند، جايگزين بيت چسبنده مي شود و اگر ۵۴-۵ EA + ED – EC باشد تمام بيت هاي A * B جايگزين يك بيت چسبنده مي گردند. بنابر اين penaity جريمة كليع ۵۰ درصد افزايش در پهناي adder مي باشد كه در عوض، زمان اجراي adder را افزايش خواهد داد. به هر حال توجه كنيد كه ۵۳ بيت بالاي adderتنها لازم است قادر به افزايش محتويات اصلي ۵۳ بيت باشد (اگر يك Carry از۱۰۶ بيت پائيني تكثير يابد).
مسير از محصول مدار گردشي در شكل ۱۶ – ۶ به مضرب در سمت راست زماني بكار مي رود كه محاسبه اي نظير (xy + z) + AXB انجام مي شود. مسير از محصول مدار نرمال سازي به مضرب سمت چپ زماني بكار مي رود كه محاسباه اي نظير (X * Y + Z) + C انجام مي شود. در اين مورد مرحلة گرد كردن براي (A * B + C) در زماني مشابه با ضرب در D با افزودن محصول نسبي ۱nn * D به درخت CSA انجام مي گيرد.
• ۶ – ۶ تنظيم مضرب ها در عمل اساسي (توليد محصولات نسبي و جمع) ممكن است ظاهر شوند. در اين روش، از افراطب overhead كه بخاطر كنترل هاي جداگانة اين دو عمل است جلوگيري مي كنيم و بنابر اين سرعت ضرب را بالا مي بريم. اين مضرب ها كه شامل سلولهاي يكساني است كه قارد به تشكيل يك محصول نسبي جديد و افزودن آن به محصول نسبي جمع شده از قبل مي باشد، مضرب هاي كناري ناميده مي شوند. واضح است كه هر سودي در سرعت، به هزينه سخت افزار
اضافي بدست مي آيد. ويژگي مهم ديگر تنظيم مضرب ها اين است كه آنها مي توانند براي حمايت سرعت بالاي لوله كشي بكار روند. براي نشان دادن عمل تنظيم يك مضرب، متوازي الاضلاع ۵ * ۵ نشان داده شده در شكل ۱۷- ۶ را آزمايش مي كنيم كه شامل ۲۵ بيت محصول نسبي به شكل a4 . xjاست كه به طور صحيحي مرتب شده است. يك استنباط مستقيم از تنظيم مضرب، دو محصول نسبي نخست را پس از تنظيم صحيح جمع مي كند. نتايج رديف اول سپس با ad .xz به صورت aD .xz … و ۲۲ در رديف دوم جمع مي شود و …. سلول اصلي براي هر تنظيم مضرب، يك FA مورد قبول يكي از محصولات نسبي جديد (ai . xi) ، يك بيت از محصول نسبي از قبل جمع شده و يك carry – in – bit است. يك نمودار block از يك تنظيم ۵*۵ براي اعداد بدون علامت، در شكل ۱۸ – ۶ ترسيم شده است. در ۴ رديف اول ، هيچ تكثير افقي carry وجود ندارد. به عبارت ديگر، يك نوع افزايش carry – save در اين رديف ها انجام مي گيرد و محصول سبي جمع شده شامل جمع متوسط و بيت هاي carry است.
تنها در رديف آخر ، تكثير افقي carry مجاز است. رديف آخر سلولها در شكل يك ripple carry – adder است كه مي تواند با يك two – operand adder سريع جايگزين شود (اگر زمان اجراي كلي مطلوب باشد) تنظيم مضرب در شكل ۱۶ – ۶ بايد براي ضرب اعداد علامت دار در دو تكميل عدد نويسي اصلاح شود، چون بيت هاي محصولي نظير a4 .xo و ao . x4 ، وزن منفي دارند و بايد كسر شوند نهجمع . يك روش براي كنترل صحيح ۸ بيت محصول نسبي وزن شدة منفي در يك ضرب ۵*۵ بيتي، در شكل ۱۹- ۶ ترسيم شده است. بيت ها با وزن منفي. با يك دايرة كوچك به جاي يك فلش، نشان داده مي شوند. اين بيت ها بايد بجاي جمع ، كسر شوند. سلولهاي با۳ محصول مثبت معمولاً FAS هستند و در شكل با I نشان داده مي شوند. سلولهاي با يك دادة منفي واحد و دو دادة مثبت ، با II نشان داده مي شوند. مجموع ۳ داده از يك سلول نوع II مي تواند از ۱- تا ۲ متغير باشد. اين مستلزم اين است كه محصول ديجيتالي C ، وزني معادل با ۲+ داشته باشد و محصول عمودي S وزن ۱- داشته باشد. عمل جبري يك سلول نوع II به وسيلة معادله با تمام داده هاي منفي نشان داده تشريح مي شود و به طور منفي وزن C و محصولات S را مي گيرد. اين سلول اعداد۱- را در داده هايش مي شمرد و اين عد را از طريق محصولات C و S نشان مي دهد. عمل منطقي آن مانند سلول نوع I است و بنابر اين، اجراهاي gate ورودي آنها يكسان است. اين ، تشريح كنندة دليل علامت گذاري آنها به صورت I , I است . همچنين اجراهاي ورودي سلولهاي نوع II و II يكسان هستند. شيوة ديگر براي طرح يك ضرب منظم براي ۲ مؤلفة operands، استفاده از الگوريتم Booth است. يك مضرب طبق اين الگوريتم شامل n رديف از سلولهاي اصلي است كه n ، تعداد بيت هاي مضرب است. هر رديف قارد به جمع يا كسر مضربهاي مرتب شدة صحيح به محصول نسبي جمع شدة قبلي است. سلولها در رديف C ، جمع يا كسر يا تنها تبديل را بسته به تعداد xi و بيت مرجع مناسب انجام مي دهند. اين مضرب در شكل ۲۰ – ۶ براي operands 4 بيت داده شده است. سلول اصلي در اين مضربع يك مدار كنترل شدة جمع / كسر / تبديل است كه در شكل ۲۰ – ۶ الف) ترسيم شده است [۱۲] . علامت هاي D , H علامت هاي كنترل نشان دهندة نوع عمل براي اجرا توسط رديف متناظر سلولهاي CASS است. اگر H ، صفر باشد هيچ جبري انجام نمي گيرد و بنابر اين بيت محصول نسبي جديد كه توسط Pwt نشان داده شده است برابر با بيت قبلي است.
اگر H=1 باشد يك عمل جبري انجام گرفته است (توليد يك pwt جديد). نوع عمل جبري بوسيلة علامت D نشان داده مي شود. اگر D=0 باشد، آنوقت بيت مضروب كه توسط a نشان داده مي شود، به pin با Q اضافه مي شود كه به عنوان يك بيت حمل وارد شونده از سلول مجاور به سمت راست است. سپس سلول، pont و C و t را به عنوان حمل خارج شونده به سلول بعدي در سمت چپ توليد مي كند. اگر D=1 باشد ، آنوقت بيت مضرب (a) از pin با Q كم مي شود كه به عنوان يك borrow وام خارج شونده است. بنابر اين معادلات قانوني براي c , t , t , p چنين است [۱۲] : pat = pin @ (a.H) @ (Q,.H) و Cat = (oin @ D) . (attim) + A . Gin .
دانلود فایل کامل بررسی فنون ديگري براي جمع آوري محصول Partial
در قالب فایل word و متشکل از 23 صفحه قابل ویرایش
در قالب فایل word و متشکل از 23 صفحه قابل ویرایش